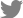Pointwise Modeling for Predicting Visual Field Progression in Korean Glaucoma Patients

Jae Hyun Kim; Sang Woo Moon; Choongrak Kim; Jiwoong Lee

doi:10.3341/jkos.2022.63.11.918

J Korean Ophthalmol Soc > Volume 63(11); 2022 > Article

녹내장성 시야결손의 점별 모델링: 초기 역치 및 중심 시야에 따른 지수형 모델의 효용

Original Article

Journal of the Korean Ophthalmological Society 2022;63(11):918-927.

Published online: November 15, 2022

DOI: https://doi.org/10.3341/jkos.2022.63.11.918

녹내장성 시야결손의 점별 모델링: 초기 역치 및 중심 시야에 따른 지수형 모델의 효용

김재현¹, 문상우¹, 김충락², 이지웅¹

¹부산대학교 의과대학 안과학교실

²부산대학교 통계학과

Pointwise Modeling for Predicting Visual Field Progression in Korean Glaucoma Patients

Jae Hyun Kim, MD¹, Sang Woo Moon, MD¹, Choongrak Kim, PhD², Jiwoong Lee, MD, PhD¹

¹Department of Ophthalmology, Pusan National University School of Medicine, Busan, Korea

²Department of Statistics, Pusan National University, Busan, Korea

Address reprint requests to Jiwoong Lee, MD, PhD Department of Ophthalmology, Pusan National University School of Medicine, #179 Gudeok-ro, Seo-gu, Busan 49241, Korea
Tel: 82-51-240-7326, Fax: 82-51-240-7434 E-mail: glaucoma@pusan.ac.kr

Received April 25, 2022 Revised August 21, 2022 Accepted October 24, 2022

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

국문초록

목적

한국인 녹내장 환자의 시야검사 각 지점의 변화를 분석하여 회귀 모델의 적합도와 예측 성능을 비교하였다.

대상과 방법

6년 이상 시행한 시야검사가 10회 이상인 개방각녹내장과 녹내장의증 환자에서 시야검사 각 지점에서 시간에 따른 역치값 변화에 선형, 지수형, 다항형 회귀분석을 시행하였다. 평균제곱근오차(root mean squared error, RMSE)를 이용하여, 세 모델의 적합도를 비교하였고, 첫 5년의 시야검사로 모델 추정 후, 1, 2, 3, 5년 후의 역치값을 예측하여 예측 성능을 비교하였다. 중심부와 주변부 영역 및 초기 역치값에 따라 예측 성능을 비교하였다.

결과

280명 439안의 평균 경과 관찰 기간과 시야검사 개수는 9.64년과 13.02개였다. 적합도 RMSE는 다항형이 가장 낮았다(p<0.001). 1년 예측에서 선형이, 3, 5년 예측에서 지수형의 RMSE가 가장 낮았다(모든 p<0.001). 1, 2년 예측 시, 초기 역치값 0-7 decibel (dB)에서 지수형이, 20-27 dB에서 선형이 RMSE가 가장 낮았다(모든 p<0.001). 선형과 지수형 모델을 비교하였을 때, 시야 주변부 1년 예측에서 선형이, 3, 5년 예측에서 지수형이 RMSE가 더 낮았다(모든 p<0.001). 시야 중심부 2년 예측부터 지수형의 RMSE가 선형보다 더 낮았다(모든 p≤0.015).

결론

한국인 녹내장성 시야결손의 점별 분석에서 단기 예측 시에 선형이, 장기 예측 시에 지수형이 성능이 우수하였다. 중심부 시야와 초기 역치값이 낮은 경우에는 지수형의 예측 성능이 선형보다 우수하였다.

Keywords: Exponential, Glaucoma, Pointwise trend-based analysis, Regression, Visual fields

ABSTRACT

Purpose

To evaluate the utility of pointwise modeling for predicting visual field (VF) progression in Korean glaucoma patients.

Methods

Open-angle glaucoma or glaucoma suspect patients with VFs ≥ 10 times, who were followed-up for ≥ 6 years, wereincluded. Linear, exponential, and polynomial regression of threshold values at each test point against time were performed. Model fit was evaluated based on root mean squared error (RMSE) for the entire longitudinal VF series. To evaluate prediction ability, VFs from the first 5 years were used to estimate model parameters, followed by calculation of threshold values for 1, 2, 3, 5 years to obtain RMSE. Prediction ability was compared regarding initial threshold value and also central and peripheral VF area.

Results

Four hundred thirty-nine eyes (280 patients) were included. The mean follow-up duration and number of VF tests were 9.64 years and 13.02, respectively. When fitting the entire VF series, polynomial model had the lowest RMSE (p < 0.001). For 1-year predictions, linear model had the lowest RMSE, while exponential model had the lowest RMSE for 3- and 5-year predictions (p < 0.001). For 1- and 2-year predictions, exponential and linear models had the lowest RMSEs, with initial sensitivities of 0-7 and 20-27 decibel (dB), respectively (p < 0.001). Compared to exponential model, linear model had lower RMSE for 1-year, but higher RMSE for 3- and 5-year at peripheral VF area (p < 0.001). For central VF area, exponential model had lower RMSEs for 2-, 3-, and 5-year predictions compared to linear model (p ≤ 0.015).

Conclusions

The linear model outperformed the exponential model for short-term predictions, while the exponential model was better for long-term predictions. The prediction performance of the exponential model was superior to that of the linear model for central VFs, and for test points with lower initial sensitivities.

Keywords: Exponential, Glaucoma, Pointwise trend-based analysis, Regression, Visual fields

녹내장이란 특징적인 시신경손상과 시야결손이 진행하는 질환이다. 녹내장성 시야결손의 진행을 발견하는 것은 녹내장 환자의 치료를 결정하는 데 있어서 매우 중요하며, 현재 표준 자동시야검사(standard automated perimetry)를 이용한 시야 평가가 녹내장성 시야결손의 진행을 확인하는 표준 검사 방법으로 사용되고 있다[1]. 녹내장성 시야결손의 진행을 판별하는 기준으로 다양한 방법이 제시되어 왔는데, Advanced Glaucoma Intervention Study (AGIS), Collaborative Initial Glaucoma Treatment Study (CIGTS), Early Manifest Glaucoma Trial (EMGT), Ocular Hypertension Treatment Study (OHTS)와 같은 대규모 무작위 임상시험들이 시야검사의 변수들을 이용하여 제시한 rule-based criteria에서부터 Humphrey visual field analyzer에서 제공하는 Glaucoma progression analysis와 같은 event-based analysis가 진행 판별에 이용되고 있다[2-6]. 하지만 이러한 방법들은 시야결손의 변화율(rate of change)에 대한 정보를 제공하지 못하며, 빠른 시야결손을 보이는 환자에게는 조기에 적극적 치료를 시행하는 것이 중요하므로 시야결손의 변화율 확인을 위한 trend-based analysis가 연구 및 개발되었다.[7]. Visual field index (VFI) 와 mean deviation (MD)과 같이 global index를 이용한 global trend-based analysis가 있는 반면, 시야검사의 각 지점에 대하여 시야결손의 변화율을 계산하는 pointwise trend-based analysis도 있다[8-10].

Pointwise trend-based analysis의 경우, 시야검사의 각 지점에서 시간에 따른 시야결손의 변화를 다양한 회귀 모델을 통해 분석하였는데, 대표적으로 선형(linear) 모델이 가장 많이 연구되었다[11,12]. 이 외에도 지수형(exponential), 로그형(logistic), 다항형(polynomial)과 같은 다양한 회귀 방법을 통하여 모델의 적합 정도뿐만이 아니라 예측 성능도 비교되었다[12-16]. 특히, Chen et al [14]과 Caprioli et al [13]은 시야검사의 각 지점에 따라 시야결손의 변화율이 다를 것이라는 가정 하에 다양한 회귀 모델을 병합하여 pointwise trendbased analysis를 시도하였다.

아시아 인종은 다른 인종에 비해 근시 등의 위험인자 분포가 높고 정상안압녹내장 등의 유병률이 유의하게 높다[17,18]. 하지만 현재까지 아시아인을 대상으로 녹내장성 시야결손 변화에 대해 시야검사의 각 지점에서 시간에 따른 회귀분석을 시행한 연구가 부족하다. 이에 본 연구에서는 한국인 녹내장 환자에 있어서 표준자동시야검사법의 각 검사 지점에서의 시간에 따른 녹내장성 시야결손 변화를 선형(linear), 지수형(exponential), 다항형(polynomial)의 회귀분석을 통하여 모델에 적합시키고 이후 변화를 예측해보고자 한다.

대상과 방법

대상

6년 이상 경과 관찰하였으며 시행한 시야검사의 횟수가 10회 이상인 녹내장 환자들을 대상으로 연구를 시행하였다. 신뢰도 지표에서 주시 상실이 30% 이하, 가음성 반응이 30% 이하, 가양성 반응이 15% 이하인 시야검사만 분석에 포함되었다. 시야검사의 학습 효과를 배제하기 위해 초기 2회의 시야검사는 분석에서 제외하였다[19,20]. 만약 시야검사의 한 지점에서의 초기 3회의 역치값이 모두 0 decibel (dB)인 경우 그 지점은 분석에서 제외되었다. 모든 시야검사는 Humphrey Field Analyzer (Carl Zeiss Meditec Inc, Dublin, CA, USA)의 24-2 SITA standard 측정법으로 시행되었고, size III white 시표가 사용되었다. 분석에는 시야검사의 각 검사 지점(test location)에서의 역치값(threshold value, THV)이 dB 단위로 이용되었다. 본 연구는 생명윤리심의위원회(Institutional Review Board)로부터 승인을 받았으며(승인 번호: 2203-025-113) 검사와 분석 과정은 Declaration of Helsinki에 의거하여 실행되었다.

회귀 모델

시야검사의 두 군데의 맹점을 제외한 각 지점에서의 시간에 따른 역치값(dB)의 변화를 선형(linear), 지수형(exponential), 다항형(polynomial)의 세 가지 방식으로 회귀분석을 시행하였다. 각 모델들의 수학적 회귀식은 다음과 같다(Fig. 1).

선형(linear): y = α + βx where x: time (1)

지수형(exponential): Iny = α + βx where x: time (2)

다항형(polynomial): y = α + β₁x + β₂x² where x: time (3)

종속변수는 역치값(y) (dB), 독립변수는 시간(x) (년), α, β, β₁, β₂는 회귀분석을 통해 산출되는 계수이다. 회귀 모델은 최소제곱법을 이용하여 산출되었다.

모델 적합

시야검사의 각 지점에서 전 기간의 역치값이 각 모델의 적합도 평가(goodness of fit)를 위해 사용되었다. 오차는 모델의 추정값(Z^)과 실제 역치값(z)의 차이로 정의한 후, 평균 제곱근 오차(root mean squared error, RMSE)를 이용하여 시야검사 각 지점에서의 세 모델의 적합도를 비교하였다.

평균 제곱근 오차(root mean squared error, RMSE):

1n∑i=1n(zi-z^i)2

where z: actual THV, z^ : estimated THV

모델 예측

모델을 통한 역치값 예측을 위해 초기 5년간의 시야검사가 모델 계수를 추정하는데 사용되었다. 추정된 모델을 이용하여 이후 1년, 2년, 3년, 5년 후의 역치값을 예측하였다. 추정된 역치값이 음수인 경우 0 dB로 조정하였으며, 예측 역치값이 상승되는 경우에는 이전 4개의 검사 값의 평균값으로 대체하였다. 1년, 2년, 3년, 5년 후의 역치값이 결측인 경우, 선형보간법(linear interpolation)을 이용하였다[14]. 예측 오차는 모델의 예측값과 실제 역치값의 차이로 정의한 후, RMSE를 이용하여 시야검사의 각 지점에서의 각 시점(1년, 2년, 3년, 5년 후)에서 세 모델의 예측 성능을 비교하였다. 더불어 시야검사 각 지점들을 초기 역치값에 따라 묶어 각 초기 역치값 구간에서 세 모델의 예측 성능을 비교하였다. 이후 시야검사 52개 검사 지점을 중심부 12지점 및 주변부 40지점으로 나누어 각 부위에서 세 모델의 예측 성능을 비교하였다.

통계 분석

선형, 지수형, 다항형 회귀의 RMSE는 일원분산분석(one-way ANOVA)을 이용하여 비교하였다. 이후 사후 검정을 위해서 본페로니 교정(Bonferroni correction) 방법을 이용한 대응 표본 T검정을 실시하였다. 또한, 시야검사 지점에 따른 선형(Linear)과 지수형(Exponential) 회귀의 RMSE 비교에는 대응표본 T검정을 사용하였다. 모델 적합, 예측 및 RMSE 비교에 대한 통계 분석은 R (4.1.1 버전) 프로그램을 이용하였다.

결 과

총 환자 280명의 439안이 본 연구에 포함되었다. 최초 시야검사 시의 평균 나이는 60.66 ± 14.60세, 평균 경과 관찰 기간은 9.64 ± 2.14년이었다. 환자당 분석에 사용된 평균 시야검사 개수는 13.02 ± 2.49였고, 분석에 사용된 시야검사 지점의 개수는 21,981개였다. 최초 그리고 마지막 시야검사의 평균 MD는 각각 -5.95 ± 5.48 dB, -6.56 ± 6.94 dB이었고, 그 분포 변화는 Figure 2와 같다. 최초 시야검사의 평균 pattern standard deviation은 5.45 ± 4.33 dB, 평균 VFI는 87.18 ± 16.87%였다(Table 1).

모델 적합

시간에 따른 시야검사 전체를 이용하여 선형, 지수형, 다항형 모델의 세 가지 방식으로 모델 적합을 시행하였다. 세 모델을 비교하였을 때, 다항형 모델이 가장 낮은 RMSE를 보였다(p<0.001, Table 2).

초기 역치값에 따라 층화하였을 때, 초기 역치값이 증가할수록 RMSE가 감소하는 경향을 보였다(Pearson coefficient=-0.491,p<0.001). 초기 역치값에 따라 층화하여 세 모델의 적합을 비교하였을 때, 다항형 모델이 모든 초기 역치값 층화 그룹에서 가장 낮은 RMSE를 보였다(p<0.001, Fig. 3).

모델 예측

초기 5년간의 시야검사를 이용하여 모델을 추정한 뒤 1년, 2년, 3년, 5년 후의 역치값을 예측하였을 때, 다항형 모델의 RMSE가 가장 높았다(p<0.001).

지수형과 선형 모델을 비교하였을 때, 1년 후의 예측 RMSE는 선형 모델이 더 낮았고(p<0.001), 2년 후의 예측 RMSE는 두 모델 사이에 차이가 없었다. 3년, 5년 후의 예측 RMSE는 지수형 모델이 선형 모델보다 더 낮았다(모든 p<0.001) (Table 3).

각 예측 년도마다 초기 역치값에 따라 층화하여 세 모델의 RMSE를 비교하였다. 1, 2년 예측의 경우, 초기 역치값 0-7 dB 구간에서는 지수형 모델이, 20-27 dB 구간에서는 선형 모델의 RMSE가 가장 낮았다(모든 P<0.05) (Fig. 4A). 3년 후 예측의 경우, 초기 역치값이 0-11 dB, 28-31 dB인 구간에서 지수형 모델이 가장 낮은 RMSE를 보였다(모든p<0.05). 5년 후 예측의 경우 4-7 dB을 제외한 모든 구간에서 지수형 모델이 가장 낮은 RMSE를 보였다(모든 p<0.05) (Fig. 4B).

시야검사 52개 지점을 중심부 12개 지점과 주변부 40개 지점의 두 영역으로 나눈 후, 각 영역에서 선형과 지수형 모델의 예측 RMSE를 비교하였다(Table 4). 1년 차 예측에서 주변부 시야에서는 선형 모델의 RMSE가 지수형 모델보다 더 낮았고(p<0.001), 중심부 시야에서는 두 모델 간의 RMSE 차이가 없었다. 2년 차 예측에서 주변부 시야에서는 두 모델 간의 차이가 없었으나, 중심부 시야에서는 지수형 모델의 RMSE가 선형모델보다 더 낮았다(p=0.015). 3, 5년 차 예측에서 중심부와 주변부 시야 모두에서 지수형 모델의 RMSE가 선형 모델보다 더 낮았다(모든 p<0.001).

시야검사 각 지점마다 선형과 지수형 모델의 예측 RMSE를 도출한 후, 중심부와 주변부로 영역을 나누어 선형과 지수형 모델 사이에 통계적으로 유의한 RMSE 차이가 있는 지점의 개수를 비교 분석하였다(Fig. 5). 예측 기간이 길어질수록 지수형 모델이 우세한 지점의 수가 증가하였다. 1년 차 예측에서 중심부 12개 지점 중 1개 지점(8.33%)에서 지수형 모델의 RMSE가 선형 모델보다 더 낮았고, 주변부 40개 지점 중 3개 지점(7.5%)에서 선형 모델의 RMSE가 지수형 모델보다 더 낮았다. 2년 차 예측에서 중심부 12개 지점 중 3개 지점(25%)과 주변부 40개 지점 중 2개 지점(5%)에서 지수형 모델의 RMSE가 선형 모델보다 더 낮았다. 3년 차 예측에서 중심부 12개 지점 중 4개 지점(33.3%)과 주변부 40개 지점 중 2개 지점(20%)에서 지수형 모델의 RMSE가 선형 모델보다 더 낮았다. 5년 차 예측에서 중심부 12개 지점 중 7개 지점(58.3%)과 주변부 40개 지점 중 21개 지점(52.5%)에서 지수형 모델의 RMSE가 선형 모델보다 더 낮았다.

고 찰

본 연구 결과에 따르면 시간에 따른 시야검사 역치값을 선형, 지수형, 다항형 회귀 모델을 이용하여 각각 적합 시에 다항형 모델이 가장 좋은 적합을 보였으며, 초기 역치값이 높을수록 더 좋은 적합을 보였으나, 예측 시에는 다항형 모델이 가장 낮은 성능을 보였다.

선형과 지수형 모델의 예측을 비교하였을 때, 단기 예측은 선형 모델이 더 우수하였으나, 장기 예측 성능은 지수형 모델이 더 우수하였다. 최초 시야검사의 역치가 낮을수록 지수형 모델이, 높을수록 선형 모델이 우수한 예측 성능을 보였다. 시야 주변부의 단기 예측에는 선형 모델이 더 우월하였으나, 장기 예측에서는 지수형 모델이 더 우수하였다. 시야 중심부 예측에서는 지수형 모델이 선형 모델보다 더 뛰어난 성능을 보였다.

선형, 지수형, 다항형 모델을 이용하여 시야검사 전 구간에 대하여 적합을 시행 시에 다항형 모델이 가장 좋은 적합도를 보였다. 그 이유는 다항형 모델이 모델 회귀분석을 할 때 선형이나 지수형 모델에 비해서 1개 더 많은 계수를 가지고 있기 때문이다[21]. 다항형 뿐만이 아니라 로그형 모델을 이용하여 적합을 시도한 연구에서도 로그형 모델이 선형이나 지수형 모델에 비하여 모델 회귀 시에 1개 더 많은 계수를 가지므로 가장 뛰어난 적합도를 보였다[14]. 하지만 적합도가 가장 높은 모델이 가장 좋은 예측을 하는 것은 아니다. 이를 통계적으로 과적합의 문제라고 하며, 본 연구와 더불어 다른 시야검사 모델링 연구에서도 가장 좋은 적합을 보인 모델이 예측에서는 우수한 성능을 보이지 않았다[21,22].

예측 성능에 관하여 선형과 지수형 모델 중 어느 모델이 더 우수한지에 대해서 여러 논문들이 다양한 결과를 제시하였다. McNaught et al [22]과 Bryan et al [23]은 지수형 모델과 비교하여 선형 모델이 예측 성능이 더 우수했다고 보고하였다. McNaught et al [22]의 연구는 본 연구의 1-2년 차 예측과 비슷한 시기에 예측을 시도하였고, 이 연구는 1년 차 예측에서 선형 모델이 우수한 성능을 보인 본 연구 결과와 유사한 결과를 보였다. Bryan et al [23]의 연구에서는 본 연구의 대략 2-3년 차 예측에 해당하는 시기에 예측을 시행하여 선형 모델의 예측 성능이 더 우수함을 보였고, 이는 본 연구 결과와는 일치하지 않았다.

진행된 녹내장 환자들을 대상으로 시야결손 진행을 예측한 AGIS 연구들에서 선형 모델에 비해 지수형 모델이 예측에 더 우수한 성능을 보였다[13,14,16]. 이에 본 연구에서도 1, 2년 후의 단기 예측에서 초기 역치값이 낮았던 지점(0-7 dB)에서는 지수형 모델이, 초기 역치값이 높았던 지점(20-27 dB)에서는 선형 모델이 더 예측 성능이 뛰어났다. 초기 역치값이 높았던 지점이라도 5년 후의 장기 예측에서는 지수형 모델이 우수한 성능을 보였다. Chen et al [14]은 환자의 녹내장성 시야결손의 단계가 시야검사 상의 실명(perimetric blindness)을 향해 가는 경우, 점근적인 양상(asymptotic trend)을 따르기 때문에 지수형 혹은 로그형 같은 회귀 모델이 더 적합할 것이라고 하였다. 이렇게 낮은 초기 역치값을 가진 경우 혹은 장기 예측인 경우에서 시야검사 악화 양상이 점근적인 양상을 띄는 이유로는 시야검사 역치값이 0 dB이라는 하한(floor)을 가지고 있으며 역치값이 낮은 구간에서는 신호 대 잡음비(signal-to-noise ratio)가 낮아 검사 결과의 변동성(fluctuation)이 높기 때문인 것으로 설명된다[11,14].

시야검사 지점을 중심부와 주변부로 나누어 선형과 지수형 모델의 예측 성능을 비교하였을 때, 주변부의 경우 예측 초기에는 선형 모델이 우수하였고 이후 두 모델 사이에 차이가 없어진 뒤 장기 예측에서는 지수형 모델이 우수하였다. 반면에 중심부는 1년 단기 예측에서는 두 모델의 성능 차이가 없었고 2년차 예측부터 지수형 모델이 더 우수하였다. 1년 단기 예측에서도 중심부 12개 지점 중 1개 지점(8.33%)에서 지수형 모델의 예측 성능이 선형 모델보다 우월하였고, 선형 모델의 예측 성능이 더 우월한 지점은 없었다.

정상안압녹내장의 경우 원발개방각녹내장에 비해 시야 결손의 진행이 시야의 중심부에서 더 자주 발생하고, 동양인에서 이런 정상안압녹내장의 비율이 높은 것으로 알려져 있다[17,24-26]. 더불어 근시를 동반한 녹내장의 경우 유두황반섬유(papillomacular bundle) 부위 손상이 두드러져 중심부 시야 악화가 조기에 나타날 수 있고, 근시 또한 동양인에서 빈도가 높다[18,27-29]. 한국인을 대상으로 한 본 연구에서 정상 안압녹내장 및 근시의 비율이 높을 것으로 추정되며 이에 중심부 예측에서 지수형 모델이 선형 모델보다 더 우수했던 것으로 생각된다. 본 연구 결과를 바탕으로 중심부 손상이 호발하는 정상안압녹내장과 근시 녹내장 환자, 그리고 심한 녹내장성 시신경 손상을 가지고 있는 환자에서 선형 모델보다 지수형 모델이 녹내장 환자의 삶의 질과 관련 있는 중심부 시야 예측에 더 도움이 될 수 있을 것으로 생각된다[30].

본 연구 한계점으로는 모델을 단일 회귀식으로 구성하여 시야 악화 속도를 낮추는 녹내장수술이나 시야 역치값를 증가시키는 백내장수술 등의 영향이 구분되지 않았다는 점이다. 이를 고려하기 위해서는 추후 복합 모델(multimodal functions)을 이용한 후속 연구가 필요할 것으로 생각된다. 더불어, 본 연구에 포함된 대부분의 환자들은 지역의원에서 안압하강제를 사용하던 중에 본 연구가 시행된 병원으로 전원된 경우로 원발개방각녹내장과 정상안압녹내장을 정확히 구분하여 연구하지 못하였던 점이 한계점으로 생각된다.

본 연구는 한국인 녹내장 환자들을 대상으로 녹내장성 시야결손 진행을 선형, 지수형, 다항형의 회귀분석을 이용하여 적합시키고 예측을 시도한 연구이다. 단기 예측 시에는 선형 모델이, 장기 예측 시에는 지수형 모델의 예측 성능이 우수하였다. 그러나 중심부 시야의 경우 주변부보다 이른 시기부터 지수형 모델의 예측 성능이 선형 모델보다 더 우월하였고, 초기 시야검사의 역치값이 낮은 경우에도 높은 경우보다 이른 시기에 지수형 모델의 예측 성능이 선형 모델보다 더 우월하였다. 본 연구 결과는 향후 추가 연구를 통하여 한국인 녹내장 환자의 시야결손 진행에 대한 정보를 제공하는 데 유용하게 사용될 수 있을 것으로 생각된다.

Acknowledgments

This research was supported by a grant from Medical big data and AI-based early detection of visual dysfunction funded by Busan and managed by Busan Techno Park.

NOTES

Conflicts of Interest

The authors have no conflicts to disclose.

Figure 1.

Examples of regression models fit to the same series of threshold values at a single visual field test location. (A) Linear. (B) Exponential. (C) Polynomial.

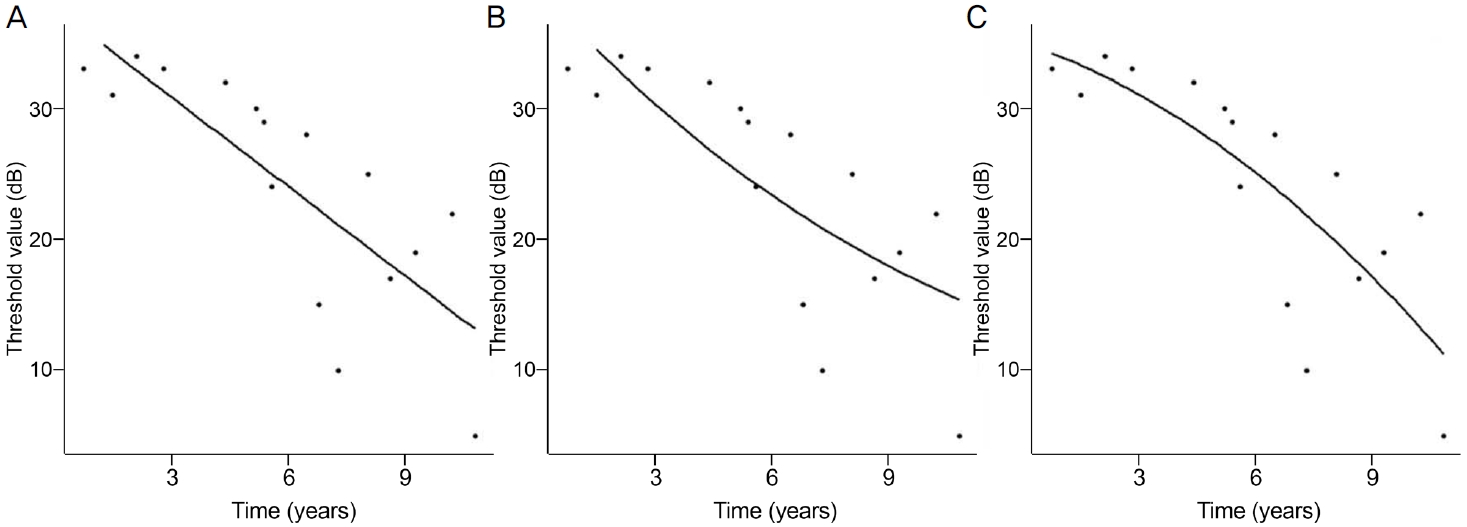
Figure 2.

Frequency distribution of initial and final visual field mean deviation for all eyes included in the study.

Figure 3.

Comparison of root mean squared error (RMSE) for fitting the model among linear, exponential, and polynomial regression model in each stratified initial threshold value group. The RMSE of the polynomial model was the lowest among the three models throughout all initial threshold value groups.

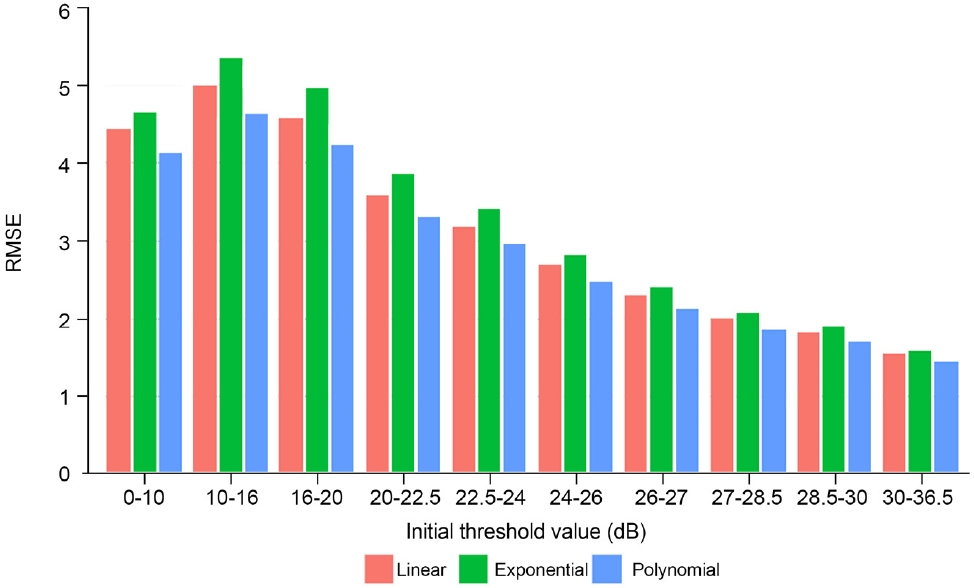
Figure 4.

Comparison of root mean squared error (RMSE) among linear, exponential, and polynomial regression model in each stratified initial threshold value group for 1-year (A) and 5-year prediction (B). Asterisk (^*) indicates the model with lowest RMSE among the three models with statistically significant difference.

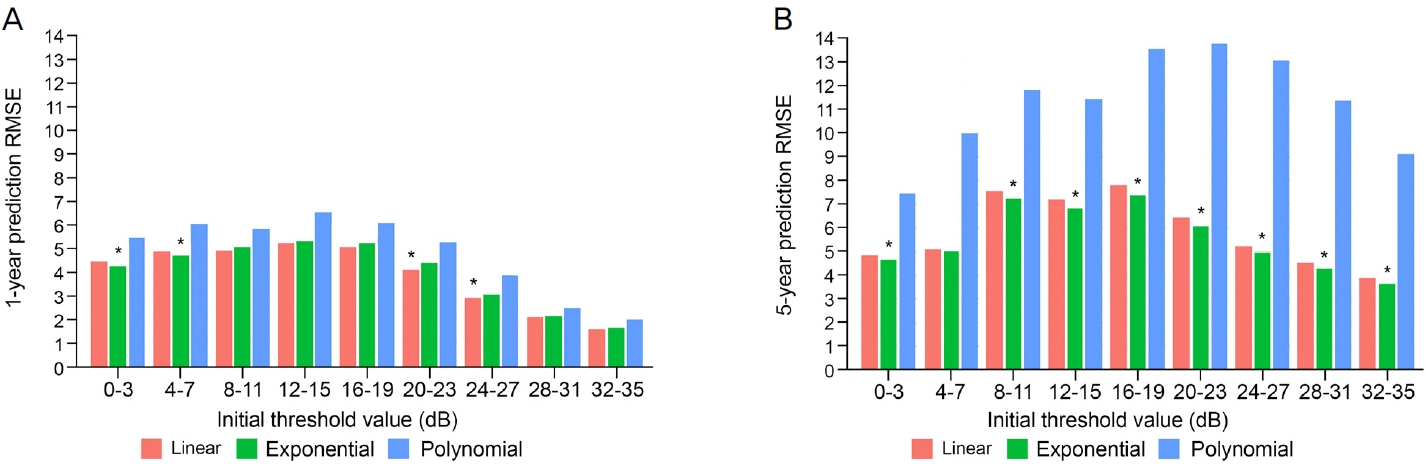
Figure 5.

Pointwise prediction root mean squared error (RMSE) of linear and exponential model indicated at each visual field test location according to the years predicted. Lighter background color at each visual field location indicates lower RMSE. White lettering of RMSE value indicates statistically significant difference between the linear and exponential model by paired t-test while black lettering indicates no significant difference between the linear and exponential model. White cross-shaped boundary identifies 12 central points in the visual field. As the predicted year increases, the number of white letterings increases in 12 central visual field test points as well as 40 peripheral visual field test points. This indicates that the prediction ability of the exponential model becomes superior to that of linear model in more visual field test points as predicted year increases.

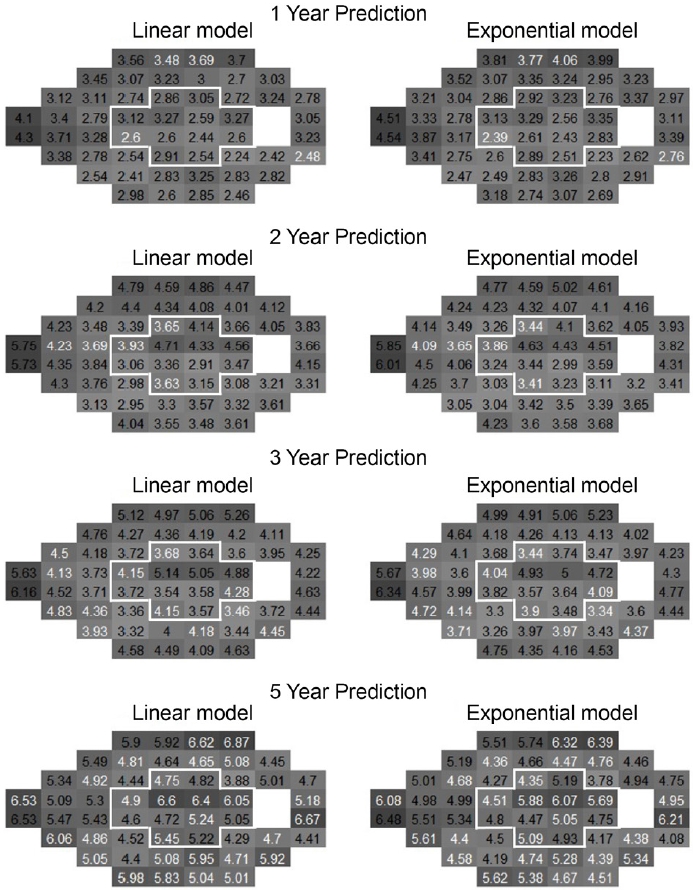
Table 1.

Demographics and main clinical data of study population

	Value
Number of eyes/patients	439/280
Age (years)	60.66 ± 14.60
Sex (male:female)	163:117
Follow-up duration (years)	9.64 ± 2.14
Number of visual field test	13.02 ± 2.49
Glaucoma type
Glaucoma suspect	89 (20.3)
Primary open angle glaucoma	331 (75.4)
Pseudoexfoliation glaucoma	16 (3.6)
Pigmentary glaucoma	3 (0.7)
Eye (right:left)	237:202
Visual acuity (logMAR)	0.37 ± 0.45
Spherical equivalent (diopters)	-2.66 ± 3.70
Central corneal thickness (µm)	549.36 ± 35.83
Axial length (mm)	24.72 ± 1.72
Pseudophakic eyes	26 (5.92)
Previous glaucoma surgery	3 (0.68)
Diabetes mellitus	50 (17.9)
Systemic hypertension	68 (24.3)
Family history of glaucoma	15 (54)
Baseline visual field parameter
Mean deviation (dB)	-5.95 ± 5.48
Pattern standard deviation (dB)	5.45 ± 4.33
Visual Field Index (%)	87.18 ± 16.87
Intraocular pressure parameter
Baseline IOP (mmHg)	15.04 ± 3.45
Mean IOP (mmHg)	15.16 ± 2.55
IOP fluctuation (mmHg)	7.41 ± 3.79
Peak IOP (mmHg)	19.10 ± 4.06
Baseline number of medications	1.20 ± 1.37

Values are presented as mean ± standard deviation or number (%) unless otherwise indicated.

LogMAR = logarithm of the minimum angle of resolution; IOP = intraocular pressure.

Table 2.

Comparison of root mean squared error (RMSE) among linear, exponential, and polynomial regression model for fitting threshold value of visual field series

Model	Average RMSE	P1^*	P2^†	P3^‡	P4^§
Linear	2.44	<0.001	<0.001	<0.001	<0.001
Exponential	2.56
Polynomial	2.26

^* p-value of multiple comparison among linear, exponential, and polynomial model by one way ANOVA;

^† p-value of comparison between linear and exponential model by paired t-test;

^‡ p-value of comparison between exponential and polynomial model by paired t-test;

^§ p-value of comparison between polynomial and linear model by paired t-test.

Table 3.

Comparison of prediction root mean squared error among linear, exponential, and polynomial regression model according to the year predicted

Years predicted	Number of visual field test points used	Prediction RMSE			P1^*	P2^†	P3^‡	P4^§
Years predicted	Number of visual field test points used	Linear	Exponential	Polynomial	P1^*	P2^†	P3^‡	P4^§
1	21,981	3.00	3.09	3.79	<0.001	0.009	<0.001	<0.001
2	20,020	3.88	3.91	6.44	<0.001	1.000	<0.001	<0.001
3	16,871	4.27	4.21	8.45	<0.001	<0.001	<0.001	<0.001
5	8,460	5.28	5.01	12.24	<0.001	<0.001	<0.001	<0.001

RMSE = root mean squared error.

^* p-value of multiple comparison among linear, exponential, and polynomial model by one way ANOVA;

^† p-value of comparison between linear and exponential model by paired t-test;

^‡ p-value of comparison between exponential and polynomial model by paired t-test;

^§ p-value of comparison between polynomial and linear model by paired t-test.

Table 4.

Comparison of root mean squared error (RMSE) of central and peripheral visual field test points between linear and exponential model according to the year predicted

	Prediction RMSE		p-value^*
	Linear	Exponential	p-value^*
1 year prediction
Central 12 points	1.80	1.79	0.339
Peripheral 40 points	2.06	2.09	<0.001
2 years prediction
Central 12 points	2.38	2.35	0.015
Peripheral 40 points	2.66	2.66	0.681
3 years prediction
Central 12 points	2.60	2.55	<0.001
Peripheral 40 points	2.92	2.88	<0.001
5 years prediction
Central 12 points	3.23	3.12	<0.001
Peripheral 40 points	3.46	3.32	<0.001

^* Paired t-test.

REFERENCES

1) Brusini P, Johnson CA. Staging functional damage in glaucoma: review of different classification methods. Surv Ophthalmol 2007;52:156-79.

2) Ederer F, Gaasterland DE, Sullivan EK; AGIS Investigators. The Advanced Glaucoma Intervention Study (AGIS): 1. Study design and methods and baseline characteristics of study patients. Control Clin Trials 1994;15:299-325.

3) Musch DC, Lichter PR, Guire KE, Standardi CL. The collaborative initial glaucoma treatment study: study design, methods, and baseline characteristics of enrolled patients. Ophthalmology 1999;106:653-62.

4) Leske MC, Heijl A, Hyman L, Bengtsson B. Early manifest glaucoma trial: design and baseline data. Ophthalmology 1999;106:2144-53.

5) Gordon MO, Kass MA. The ocular hypertension treatment study: design and baseline description of the participants. Arch Ophthalmol 1999;117:573-83.

6) Arnalich-Montiel F, Casas-Llera P, Muñoz-Negrete FJ, Rebolleda G. Performance of glaucoma progression analysis software in a glaucoma population. Graefes Arch Clin Exp Ophthalmol 2009;247:391-7.

7) Caprioli J. The importance of rates in glaucoma. Am J Ophthalmol 2008;145:191-2.

8) Bengtsson B, Patella VM, Heijl A. Prediction of glaucomatous visual field loss by extrapolation of linear trends. Arch Ophthalmol 2009;127:1610-5.

9) Bengtsson B, Heijl A. A visual field index for calculation of glaucoma rate of progression. Am J Ophthalmol 2008;145:343-53.

10) Park CS, Yoon HS, Rho SH. Characteristecs of visual field progression in normal tension glaucoma. J Korean Ophthalmol Soc 1998;39:1831-42.

11) Gardiner SK, Swanson WH, Goren D, et al. Assessment of the reliability of standard automated perimetry in regions of glaucomatous damage. Ophthalmology 2014;121:1359-69.

12) Smith SD, Katz J, Quigley HA. Analysis of progressive change in automated visual fields in glaucoma. Invest Ophthalmol Vis Sci 1996;37:1419-28.

13) Caprioli J, Mock D, Bitrian E, et al. A method to measure and predict rates of regional visual field decay in glaucoma. Invest Ophthalmol Vis Sci 2011;52:4765-73.

14) Chen A, Nouri-Mahdavi K, Otarola FJ, et al. Models of glaucomatous visual field loss. Invest Ophthalmol Vis Sci 2014;55:7881-7.

15) Nouri-Mahdavi K, Hoffman D, Ralli M, Caprioli J. Comparison of methods to predict visual field progression in glaucoma. Arch Ophthalmol 2007;125:1176-81.

16) Azarbod P, Mock D, Bitrian E, et al. Validation of point-wise exponential regression to measure the decay rates of glaucomatous visual fields. Invest Ophthalmol Vis Sci 2012;53:5403-9.

17) Stein JD, Kim DS, Niziol LM, et al. Differences in rates of glaucoma among Asian Americans and other racial groups, and among various Asian ethnic groups. Ophthalmology 2011;118:1031-7.

18) Wong YL, Saw SM. Epidemiology of pathologic myopia in Asia and worldwide. Asia Pac J Ophthalmol (Phila) 2016;5:394-402.

19) De Tarso Pierre-Filho P, Gomes PR, Pierre ET, Pierre LM. Learning effect of Humphrey matrix frequency doubling technology perimetry in patients with open-angle glaucoma. Eur J Ophthalmol 2010;20:538-41.

20) Heijl A, Bengtsson B. The effect of perimetric experience in patients with glaucoma. Arch Ophthalmol 1996;114:19-22.

21) Chatfield C. Linear Systems. In: Chatfield C, ed. The Analysis of Time Series: Theory and Practice, 1st ed. Boston: Springer, 1975;277.

22) McNaught AI, Crabb DP, Fitzke FW, Hitchings RA. Modelling series of visual fields to detect progression in normal-tension glaucoma. Graefes Arch Clin Exp Ophthalmol 1995;233:750-5.

23) Bryan SR, Vermeer KA, Eilers PH, et al. Robust and censored modeling and prediction of progression in glaucomatous visual fields. Invest Ophthalmol Vis Sci 2013;54:6694-700.

24) Ahrlich KG, De Moraes CG, Teng CC, et al. Visual field progression differences between normal-tension and exfoliative hightension glaucoma. Invest Ophthalmol Vis Sci 2010;51:1458-63.

25) Park HY, Park SH, Park CK. Central visual field progression in normal-tension glaucoma patients with autonomic dysfunction. Invest Ophthalmol Vis Sci 2014;55:2557-63.

26) Chauhan BC, Drance SM, Douglas GR, Johnson CA. Visual field damage in normal-tension and high-tension glaucoma. Am J Ophthalmol 1989;108:636-42.

27) Tan NYQ, Sng CCA, Jonas JB, et al. Glaucoma in myopia: diagnostic dilemmas. Br J Ophthalmol 2019;103:1347-55.

28) Chihara E, Tanihara H. Parameters associated with papillomacular bundle defects in glaucoma. Graefes Arch Clin Exp Ophthalmol 1992;230:511-7.

29) Kimura Y, Hangai M, Morooka S, et al. Retinal nerve fiber layer defects in highly myopic eyes with early glaucoma. Invest Ophthalmol Vis Sci 2012;53:6472-8.

30) Sun Y, Lin C, Waisbourd M, et al. The impact of visual field clusters on performance-based measures and vision-related quality of life in patients with glaucoma. Am J Ophthalmol 2016;163:45-52.

Biography

김재현 / Jae Hyun Kim

부산대학교 의과대학 안과학교실

Department of Ophthalmology, Pusan National University School of Medicine